| 特性 | 數值 |
|---|---|
| 內能變化 | ΔU |
| 熱量 | Q |
| 功 | W |
| 恆定體積熱容 | Cv |
| 定壓熱容 | Cp |
| 絕熱指數 | γ |
| 莫耳內能 | Uv |
| 比內能 | u |
| 系統 | S |
| 狀態變數 | V |
| 外延物理量 | p |
| 無窮小量 | dU |
| 微分 | δQ |
一系統內給定狀態的內能 U 可由該系統的標準狀態開始,透過能量的宏觀轉移,使得該系統的狀態由參考狀態轉變成給定狀態而決定:

$$Δ\nU = E_i$$
其中,ΔU 表示內能在給定狀態與在參考狀態下的差,而 Ei 則是用於系統由參考狀態轉變成給定狀態的各種能量。
從非相對論微觀角度來看,內能可被分為微觀位能 Umicro,pot 及微觀動能 Umicro,kin 兩個部分:
$$U_{micro,pot}, U_{micro,kin}$$
就熱力學及工程學上的實際用途來看,一般很少需要,或甚至不可能考慮一個系統的所有內含能量,如質量所含有的等價能量。一般而言,只有與研究的系統及程序有關的部分才會被包含進來。
實際上,在大多數考量的系統內,尤其是在熱力學裡,計算出所有內能是不可能的。因此,通常會為內能選定一參考零值。

內能是個外延物理量,即內能與系統之大小,或系統所含物質多寡有關。
內能的微觀動能部分取決於該系統的温度。統計力學將個別粒子半隨機的動能與構成整個系統的粒子之平均動能所關連。甚至,統計力學將微觀的平均動能與宏觀可見的系統之温度相關連。此一能量通常被指為系統的「熱能」
$$U = Σ_i p_i E_i$$
$$ΔU = Q + W$$
封閉系統裡內能變化的第二個機制為對該系統作功(英語:Work_(thermodynamics)),不論是透過改變壓力或容量所作的機械功,或是透過向系統通電等方式所作的功。
若系統不是封閉的,則改變內能的第三個機制還包括系統內物質的傳遞。其變化量 ΔUmatter 無法被分成加熱或作功這兩個部分。
若系統的加熱與作功是以與物質傳遞無關之方式在進行的,則能量的傳遞可加在內能的變化量上:
$$ΔU = Q + W + ΔU_{matter}$$
若一系統在加熱中發生了某種相變(如熔化或汽化),可觀察到該系統的温度在完成所有轉變之前都不會改變。加入系統內,卻不會改變系統温度的能量,稱之為潛能(或潛熱),與會跟温度變化相關連的顯熱相對。
因此,理想氣體的內能變化可是只透過其動能的變化來描述。在理想氣體裡,動能完全由該系統的壓力、容量與熱力學温度來決定。
$$U = U(S, V, N)$$
其中,c 為該氣體(在固定容量下)的熱容量。內部可寫成三個外延物理量(熵 S、容量 V 與質量 N)的函數,如下:
$$U = const + RNT$$
其中,const 為一任意正數,而 R 則為氣體常數。簡單可知,U 會是三個變數的線性齊次函數(亦即為這些變數的「外延」函數),且為弱凸函數。知道温度與壓力為導數
$$T = \frac {∂U}{∂S}, p = – \frac {∂U}{∂V},$$
上面內能之變化量均假定附加給系統的熱量及對系統作的功為正值,而系統對環境作的功則為負值。
一般,內能的關係式會以無窮小量的方式來表示,其中只有內能一項為全微分。對一個只進行熱力學過程的系統(即一隻交換熱與功的封閉系統),內能的變化量為
$$dU = δQ + δW$$
例如,對一非黏性流體,在該系統上所作的機械功,會與壓力 p 及容量 V 相關。
$$V = V(S, N)$$
這裡,功 W 的方向定義為從作用系統流向周圍環境的能量;熱量 Q 的傳遞方向則定義為流入作用流體之能量,並假定為一可逆過程:
$$dU = T dS – p dV$$
$$δQ = T dS$$
$$dU = C_{v}dT$$
$$C_{v} = \frac{R}{γ -1}$$
$$C_{v}$$
$$γ = \frac{5}{3}$$
對於單原子理想氣體,對於雙原子理想氣體,γ = 7/5。至於實際氣體,有:
$$C_v(T)=a+bT+…+fT^n$$
$$C_v(T)=\frac{∂U}{∂T}$$
$$dU = \frac{∂U}{∂T} dT – \frac{∂U}{∂V} dV = C_v dT + T \frac{∂S}{∂V} dV$$
若狀態方程式可知,則可算出 S 相對於 V 的偏導數。由熱力學基本關係可知,亥姆霍茲自由能 A 的微分如下:
$$dA = dU – TdS – SdT$$
A 相對於 T 與 V 之二階導數的對稱性,可給出麥克斯韋關係式:
$$- \frac{∂T}{∂V} = \frac{∂p}{∂S}$$
當處理液體或固體時,隨温度與壓力而變的變化量之公式通常會比較有用:
$$C_{pT} – C_{v} = V T \left( \frac{∂p}{∂T} \right){V} \left( \frac{∂V}{∂p} \right){T}$$
內能:系統中能量的量度
內能(符號:U)是熱力學系統中能量的量度,表示系統所有分子的動能和勢能總和。它涵蓋了系統中所有形式的能量,包括熱能、運動能、位能、化學能和原子能等。
內能的變化
內能可以通過系統與環境之間的熱量和功交換而變化。當熱量傳入系統時,內能增加;當熱量流出系統時,內能減少。當功對系統做功時,內能增加;當系統對環境做功時,內能減少。
根據熱力學第一定律,系統內能的變化等於傳入系統的熱量和對系統做功的代數和。數學式表示為:
其中:
- △U:系統內能的變化
- Q:傳入系統的熱量
- W:對系統做的功
影響內能的因素
內能受到多種因素的影響,包括:
| 因素 | 影響 |
|---|---|
| 温度 | 温度升高,分子的平均動能和位能增加,內能增加 |
| 體積 | 體積膨脹,分子的平均距離和相互作用減少,內能減少 |
| 化學成分 | 分子間的鍵能和原子間的電子組態影響內能 |
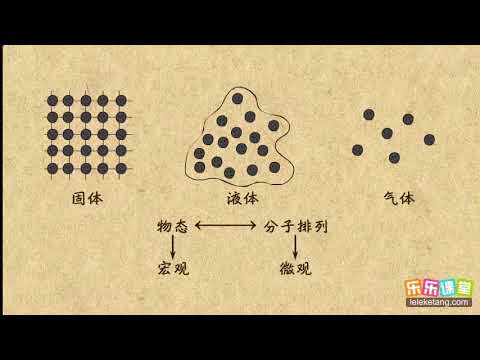
| 相態 | 物質的相態不同,分子的平均動能和自由度不同,內能也不同 |
內能應用
內能的概念在熱力學和工程領域有著廣泛的應用,包括:
- 計算熱力學系統的熱容和比熱容
- 分析熱機和冷氣機的效率
- 設計高效的能耗設備
- 理解化學反應中的能量變化
- 解釋材料的熱膨脹和熱收縮
總結
內能是熱力學系統中能量的總和,涵蓋了所有形式的能量。內能受温度、體積、化學成分和相態等因素影響。內能的變化取決於熱量和功的交換。理解內能對於分析熱力學過程和設計能源系統至關重要。
