兩條異面直線的公垂線與公垂線段

在幾何學中，兩條異面直線的公垂線與公垂線段是一些重要的概念。今天來深入地探討這些概念。

前言

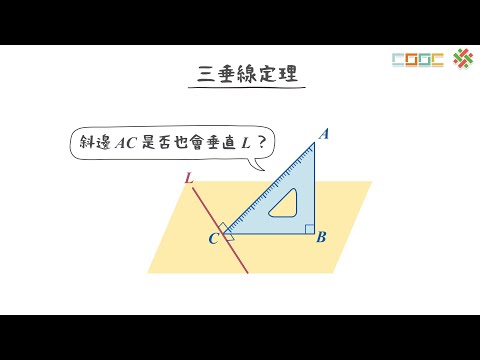
線段或直線的「公垂線」，是指同時垂直於兩條線段或直線的直線。然而，當兩條直線不存在於同一個平面上時（即異面），其公垂線則需要進一步的定義。本文將深入解釋兩條異面直線的公垂線，以及與之相關的「公垂線段」概念。

定義

1. 兩個平行平面同時垂直的直線，稱為平行平面的公垂線。公垂線夾在兩個平行平面間的部分，則稱為平行平面的公垂線段。
2. 兩條異面直線都垂直相交的直線，稱為異面直線的公垂線，公垂線與兩條直線相交的點所形成的線段，稱為異面直線的公垂線段。

性質

1. 任意兩條異面直線有且只有一條公垂線。
2. 兩條異面直線的公垂線段長（異面直線的距離）是分別連結兩條異面直線上兩點的線段中最短的一條。

定理

定理一： 任意兩條異面直線有且只有一條公垂線。

定理二： 兩條異面直線的公垂線段長（異面直線的距離）是分別連結兩條異面直線上兩點的線段中最短的一條。

常用計算方法

1. 找出（或作出）公垂線，計算公垂線段的長度。
2. 將兩條異面直線視為斜率分別為 m1 和 m2 的兩條直線，使用公式 (y2 – y1) / (x2 – x1) = (m1 – m2) / (1 + m1 * m2) 算出兩條直線的交點，再計算交點與兩條異面直線上任意一點的距離，取距離較短者即為異面直線的距離。
3. 若題目提供線段長度或線段的中點，可依題目提供的資訊推算兩條異面直線的方程式，再依上述兩種方法求解。

練習題

Q1： 求兩條異面直線 AB 和 CD 的距離，其中 A(1, 2, 3), B(4, 5, 6), C(2, 1, 4), D(5, 4, 7)。

Q2： 已知兩條異面直線 AB 和 CD 的交點為 P(1, 2, 3)， AB 的方向向量為 (1, 1, 1)，求 AC 和 PD 的夾角。

解題過程請見課本或參考書，本文不再贅述。

公垂線定義

1. 什麼是公垂線？

公垂線是一種特殊的線段，它可以幫助我們理解幾何圖形中一些重要的概念。以下是一些關於公垂線的定義：

• 定義 1： 公垂線是從一個點到一條直線的垂線段。
• 定義 2： 公垂線是兩個圖形之間最短的距離。
• 定義 3： 公垂線是兩個圖形之間的公共垂直線。

2. 公垂線的特性

公垂線具有以下特性：

• 公垂線是垂直於直線的線段。
• 公垂線的長度是垂足到直線的距離。
• 公垂線是連接曲線和直線之間最短的線段。
• 兩條線段的公垂線位於這兩條線段之間。

3. 公垂線的應用

公垂線在幾何學中有很多應用，例如：

• 判斷兩條直線是否平行: 通過檢查兩條直線的公垂線是否平行來判斷。
• 計算兩條直線之間的距離: 通過計算兩條直線的公垂線的長度來計算。
• 構造相交線段的垂線: 通過構造相交線段的公垂線來構造。

4. 公垂線的例子

以下是一些公垂線的例子：

延伸閲讀…

公垂線- 教育百科

概念,引申含義,異面直線的公垂線,定義,定理,基於 …

• 點 $A$ 到直線 $BC$ 的公垂線是線段 $AD$，其中 $D$ 是直線 $BC$ 上的垂足。
• 兩條平行線之間的公垂線是線段 $EF$，其中 $E$ 和 $F$ 是兩條平行線上任意兩點。
• 兩條相交線段 $AB$ 和 $CD$ 的公垂線是線段 $GH$，其中 $G$ 和 $H$ 是線段 $AB$ 和 $CD$ 上的垂足。

5. 公垂線的表格

公垂線	定義	特性	應用	例子
點到直線的公垂線	從一個點到一條直線的垂線段。	垂直於直線，長度為垂足到直線的距離。	判斷兩條直線是否平行，計算兩條直線之間的距離，構造相交線段的垂線。	點 A 到直線 BC 的公垂線是線段 AD，其中 D 是直線 BC 上的垂足。
兩條平行線的公垂線	兩條平行線之間的最短距離。	垂直於兩條平行線，長度相等。	計算兩條平行線之間的距離。	兩條平行線之間的公垂線是線段 EF，其中 E 和 F 是兩條平行線上任意兩點。
兩條相交線段的公垂線	連接曲線和直線之間最短的線段。	垂直於兩條線段，長度相等。	判斷兩條線段是否平行，計算兩條線段之間的距離，構造相交線段的垂線。	兩條相交線段 AB 和 CD 的公垂線是線段 GH，其中 G 和 H 是線段 AB 和 CD 上的垂足。