【八卦算法】八卦玄機盡現！揭秘五行八卦算法的奧秘

周易數推演吉凶

「元會運世」元素自邵雍「皇極經世」中衍生而來，被祝泌應用於「皇極經世鈐」中，後於「周易數」沿用作為推演吉凶的依據。

儘管「皇極經世鈐」原著並未記載該法，而且此元會運世與邵雍論述無關，僅借用於轉換數字。可見將元會運世改用其他符號，例如春夏秋冬等，也同樣可供推演。

在使用元會運世推演前，先計算「軌策數」，通常為四位或五位數字，其各數字分別代表元、會、運、世。根據這些數字的順逆進退，及五行生剋關係，判斷吉凶。

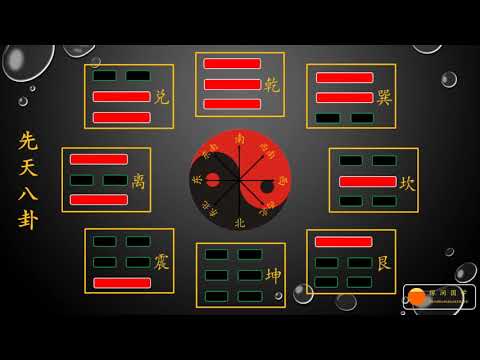
「梅花易數」分先天數與後天數。先天數根據事件變化取得數字，後轉換為卦象，使用邵雍加一倍法所得之先天八卦數，即所謂先天八卦次序圖。後天數則直接依卦象取卦，以先天八卦數換取變爻。

不管先天或後天數，「周易數」皆需推算「先天演策數」或「後天軌策數」，再根據元會運世之數推演吉凶。但「周易數」卦例中的後天數卦象混亂，有時使用先天演策數，有時使用後天軌策數。

此外，與「皇極經世心易發微」相較，「周易數」稱先天為「策數」，後天為「軌數」，與「發微」的嚴格區分不同，造成一些名詞混淆。

軌策數演算

先天演策數和後天軌策數的演算法類似，差異僅在於卦數和基準數的不同。下表整理了兩種演算法：

起算方式	先天演策數	後天軌策數
變爻在上卦	元 = 動因 x 10 + 卦因 x 0	元 = 卦因 x 10 + 動因 x 0
變爻在下卦	元 = 卦因 x 10 + 動因 x 0	元 = 動因 x 10 + 卦因 x 0

演算示例

先天演策數:

• 地天泰卦，第五爻動，上坤為8，下乾為1，原策數為180。變爻在上卦，故用第一個公式：
  元 = 0，會 = 6，運 = 3，世 = 4

• 恆卦，三爻動，上震為4，下巽為5，原策數為180。變爻在下卦，故用第二個公式：
  元 = 9，會 = 7，運 = 3，世 = 2

• 蒙卦，五爻動，上艮為7，下坎為6，原策數為168。變爻在上卦，故用第一個公式：
  元 = 9，會 = 7，運 = 6，世 = 2

後天軌策數:

• 大壯卦，五爻動，上震為3，下乾為6，後天原策數為736。動爻在五，為上卦動，故用第一個公式：
  元 = 3，會 = 0，運 = 6，世 = 4

八卦算法

八卦算法是一種基於八個三元組的隨機產生器，可用於模擬複雜現象並解決各種問題。它由 IBM 研究人員於 1996 年開發，並自那時起成為計算機科學和統計建模中廣泛使用的工具。

演算法描述

八卦算法的工作原理如下：

1. 初始化：從一個包含八個三元組的種子集合開始。
2. 重複：
   • 隨機選擇一個三元組。
   • 計算三元組的加權和並將其加入到累積和中。
   • 隨機選擇一個三元組並將其從集合中刪除。
   • 生成一個新的三元組並將其加入到集合中。
3. 返回：當累積和達到閾值或迭代次數達到指定值時，停止並返回累積和。

變異

八卦算法有許多變異，包括：

變異	描述
加權八卦	對三元組的加權和進行加權
排序八卦	在選擇三元組之前對三元組進行排序
遞歸八卦	遞歸呼叫八卦算法以探索不同的路徑

應用

八卦算法已成功應用於以下領域：

應用	描述
隨機數生成	生成隨機數
估計與模擬	估計復雜系統的特性
最佳化	求解最佳化問題
數據挖掘	發現數據中的模式

優點與缺點

八卦算法的主要優點包括：

• 效率：它是一種高效的算法，即使在大型數據集上也能快速執行。
• 準確性：它產生高質量的隨機數，適合模擬複雜現象。
• 靈活性：可以根據具體應用調整算法的參數。

然而，八卦算法也有一些缺點：